乌鸦喝水:到底怎样能喝到?
很多人小学的时候都学过“乌鸦喝水”的故事:一只乌鸦口渴了,四处找水喝。它发现一个瓶子里有水,但是够不着,于是聪明的乌鸦把石子丢进去,升高了水位,从而喝到了水。这个故事最早的出处可能是伊索寓言,名为“乌鸦和水罐”,佩里索引号为390。在伊索的
周末特辑:妙题巧解
周末特辑:妙题巧解妙题巧解(2)“1”字聚会37+37+37=111瞧,37连加三次,和便是111。全是1。你知道,连加后所得的和形成“1”字大聚会,还有哪些数?将8547, 15873, 12345679分别连加,看看它们的和各是多少?解
有趣周末:这里面有鬼!
海边的旅游胜地风景如画,在这样一个迷人的地方犯下如此愚蠢而臭不可闻的罪行实在是令人扫兴。如下图所示,这个地方有7栋乡村平房,其中4栋座落在环礁湖边(A,B,C与D),两栋在海边(F和G),一栋在中间(E),平房间彼此有小路连接,一位渔夫看见
不确定性原理的前世今生 · 数学篇(一)
在现代数学中有一个很容易被外行误解的词汇:信号 (signal)。当数学家们说起「一个信号」的时候,他们脑海中想到的并不是交通指示灯所发出的闪烁光芒或者手机屏幕顶部的天线图案,而是一段可以具体数字化的信息,可以是声音,可以是图像,也可是遥感
九个问题
1.回到原地的探险家 一个古老的谜是这样的。一位探险家向正南方走了一英里,转向正东方走了一英里,再转向正北方走了一英里。他发现自己回到了原出发地。他打了一只熊。这只熊是什么颜色的?历史悠久的答案是“白色”,因为探险家肯定是从北极点出发的
此时无声胜有声
三等分角(On Trisecting an Angle)——Rufus Isaacs在一个无穷级数中一个角的三等分(Trisection of an Angle in an Infinite Number of Steps)——Eric K
变脸六边形折纸
变脸折纸是纸制的多边形,用直的或弯的纸条折叠而成,特点是折曲时能变换面孔。要不是英国人和美国人用的笔记本纸张大小有所不同,变脸折纸也许仍未被发现,而大批一流的数学家也就无法享受分析这种玩意儿的结构给他们带来的乐趣。这一切都始于1939年秋天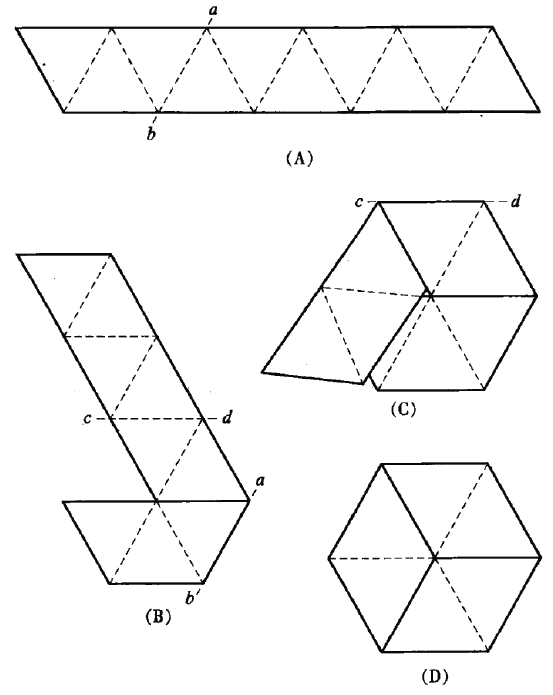
4个终于被破译的世界级密码
很多时候,一个设计精巧的密码就像数学难题一样,许许多多难以破解的密码让人青丝泛白,至今仍未见天日。不过,也有一些密码中的幸运儿,最终仍然迎来了真相大白的那天。秘密组织的手抄本密码这份超过 75000 个字母的手抄加密文件名叫 “Copial
生日悖论与生日攻击:50个人中相同生日的缘分是多少?
每个人都有生日,偶尔会遇到与自己同一天过生日的人,但在生活中,这种缘分似乎并不常有。我们猜猜看,在50个人当中,出现这种缘分的概率有多大,是10%,20%,还是50%?有人告诉我,在文章开头插入公式十分倒胃,所以我就不写计算过程,直接给出结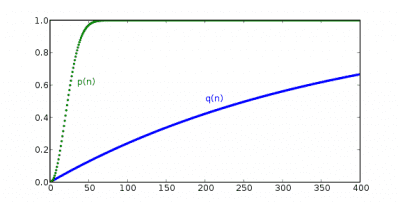
台湾论坛热门话题:? " 班上的最后一名后来都怎样了?"。昨天有位网友跟帖非常励志…
这两天台湾论坛有个热门话题: " 班上的最后一名后来都怎样了 "。昨天有位网友跟帖非常励志…(@台南阿呆仔)Via:微信公众号:涨姿势(zhangzishi_weixin)金融工程, 数学算法原文发布于宽客论坛,点击阅读原文
用数学方法识别猕猴面部特征
(封面图片来源:百度图片搜索)2015年菠萝医学生物学奖颁给了来自郑州大学生物多样性与生态研究所的路纪琪教授团队,以表彰他们用数学方法对猴子面部相似度进行了分析,并发现有血缘关系的猴子长得更像。为什么这样的研究都可以发表?它又是凭什么能获得
一根棒棒糖能舔多少口?
“棒棒糖需要舔多少口才能被完全吃掉?” 这几乎是一个世界性的问题。80年代美国的一则著名的棒棒糖广告中,一位小男孩向森林中的动物们请教这个问题,最终猫头鹰先生(Mr. Owl)告诉他说我们应该用实验来检验。猫头鹰开始实验,但是到第三口就忍不
确定你深入了解勾股定理了?
勾股定理Ⅰ(The Pythagorean Theorem Ⅰ)——改编自Chow pei suan.ching(作者不明,大约公元200年)(adapted from the Chou pei suan..ching (author un
另类视觉盛宴:无处不在的0.618
提到黄金分割 0.618,大家首先想到的必然是神秘的大自然以及那些伟大的艺术作品。其实,在数学内部,0.618 也无处不在。黄金分割常常意外地出现在一些极其简单的几何构造中,可谓是黄金分割之美的另一种视觉盛宴。在这里,我们有意略去证明过程,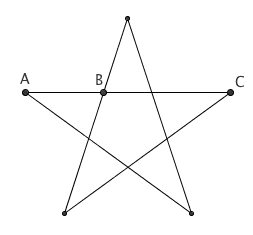
π究竟牛B在哪里?
每年的3月14日为圆周率日,而圆周率 π 就约等于 3.14,因此这一天被设为了圆周率日。世界各地的数学家和数学爱好者们欢聚一堂,歌颂赞美这个数学世界中的奇迹。大家或许会好奇,π 究竟哪点吸引人了,能够让数学家们对它痴迷到如此地步?其实,π
周末数模小教程——用Ecel制作成对条形图
(文/bkueskychen)成对条形图(或旋风图)常用于对比两类事物在不同特征项目的数据情况,例如美国总统选举中不同地区投支持票和反对票的比例情况,足球比赛中主队和客队的各项技术统计等。图表的特点是两组条形图的数据条沿中间的纵轴分别朝左右
永无止境—本罗特·曼德尔布洛特开启了分形世界的入口
本罗特·曼德尔布洛特倚靠着一幅著名的分形背景图。这幅分形图是他创造的,具有可以无限展开的结构。一个简单而充满疑惑的问题开启了一种新的几何学不同寻常的故事。英国的海岸线究竟有多长?我们可以拿出一份地图,参照它的标尺,用一把尺子来对英国海岸线的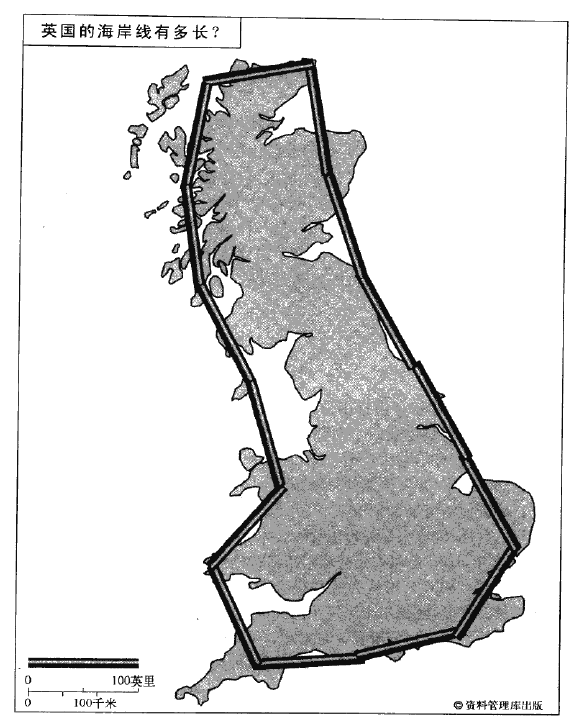
意料之外的相似与不同
不可否认,我们对意料之外的东西始终是抱有极大兴趣的,并且一旦接触,往往记忆深刻。当一部电影的结局出乎我们意料之外,即使剧情是如此地狗血,我们就会因此而记住它。就如同某些巧合,正是因为其大大出乎我们意料之外,才让我们记忆尤深。1:巧合——意料
