勾股定理Ⅰ(The Pythagorean Theorem Ⅰ)

——改编自Chow pei suan.ching(作者不明,大约公元200年)
(adapted from the Chou pei suan..ching (author unknown, circa B.C. 200?))
勾股定理Ⅱ(The Pythagorean Theorem Ⅱ)

--Bhaskara(12th century)
勾股定理Ⅲ(The Pythagorean Theorem Ⅲ)

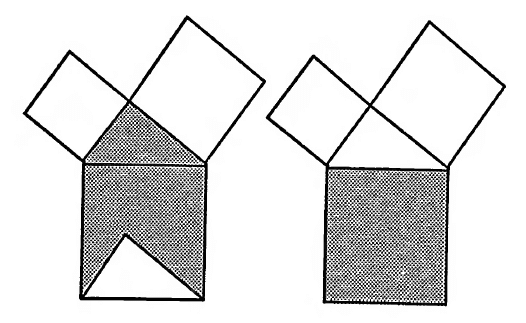
——基于欧几里得的证明(based on Euclid' proof)
勾股定理Ⅳ(The Pythagorean Theorem Ⅳ)


--H.E. Dudeney(1917)
勾股定理Ⅴ(The Pythagorean Theorem Ⅴ)
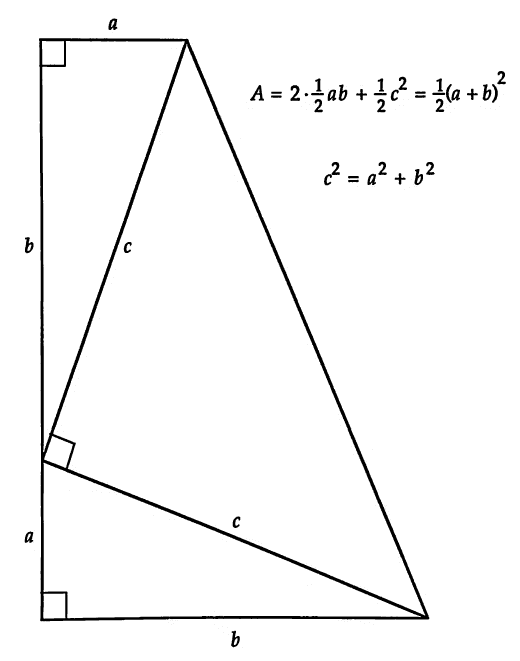
——詹姆斯·艾伯拉姆·加菲尔德(1876)【美国第20任总统】
(James A. Garfield)
勾股定理Ⅵ(The Pythagorean Theorem Ⅵ)
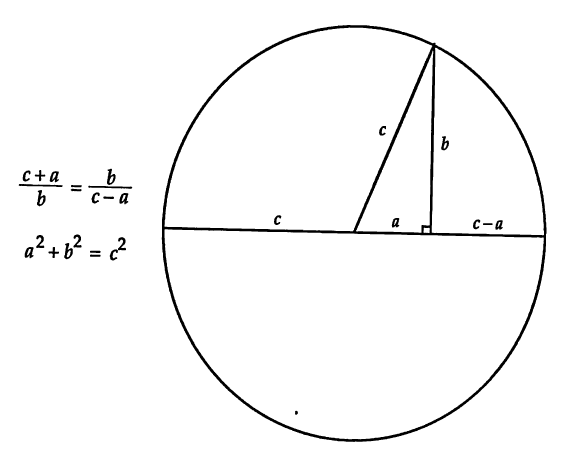
——Michael Hardy
勾股定理:a·a'=b·b'+c·c'(A Pythagorean Theorem: a·a'=b·b'+c·c' )


--Enzo R. Gentile
Via:Proofs Without Words :Exercises in Visual Thinking
Authored by Roger B. Nelsen
超级数学建模对其有节选
金融工程, 数学算法
