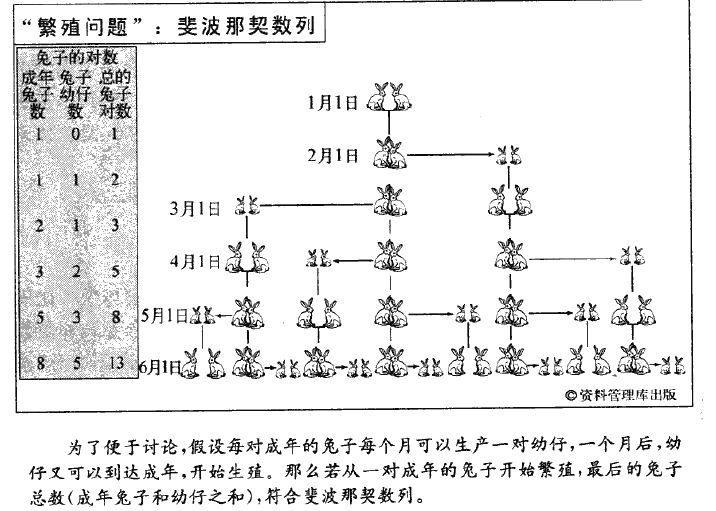
莱昂纳多在数论方面的工作起着关键性的承前启后的作用,他承接了伟大的古代数学家(比如丢番图)的成就,又开启了近代欧洲数学家(比如皮埃尔·费马)的工作。莱昂纳多最值得纪念的成就是他的《算术》一书第三部分提出的一个“兔子问题”。问题是这样的:如果一对兔子在每个月能够生产一对幼仔,而幼仔一个月后又可以开始生产,那么把一对兔子圈养在一个封闭的屋子里,供给足够的养料,一年以后,屋子里共有多少只兔子呢?
如第7页图中所示,繁殖的结果可以用一个连续相加的数列来表示,从1(单位是“对")开始,后面的数都等于在该数之前的两个数字之和。即结果是1,1,2,3,5,5,8,13,…等等。这个简的数列在许多领域都有惊人的应用。
尽管这个数列早在9世纪的时候就已经流传于印度,但是莱昂纳多将这个数列放在了一个更大的背景下,并应用到了更加广泛的数学领域之中。
自然界中的斐波那契数列
莱昂纳多之后的几个世纪,进人了文艺复兴时期。艺术家和科学家开始把目光投向现实世界,包括植物的结构、动物的躯体和人类自身。
随着人们对结构研究的深入,斐波那契数列开始应用于测量领域。
例如,植物的生长过程通常是季节性的,它们随着供给生长的阳光和水分的周期性变化而发生季节性的“暴长”,结果形成了螺旋形的叶序结构。每一部分都有一定的长度,并按螺旋状排列,以便能够留出足够的空间,让其他叶片也能得到足够的阳光。研究表明,植物的“叶序比例”通常是符合斐波那契数列的。类似的螺旋比例还广泛存在于松果、朝鲜蓟、雏菊和向日葵等植物中。
相似的螺旋也发生在动物的生长过程中。与植物生长中对空间进行螺旋切分不同的是,鹦鹉螺的贝壳在生长中保持“等角螺旋”,即在生长中贝壳内角保持不变。也就是说,鹦鹉螺的贝壳在生长中沿着一个固定的比率,逐渐长大。与之相同的结构可以在海星、沙滩银鲳,甚至其他多种蜘蛛网中发现,当然并不是所有的结构都符合斐波那契数列,但总体来说,有许多是符合的。
黄金比率
斐波那契数列同样可以应用于人类的建筑。或许因为它与生长比例协调一致,广泛符合自然法则,所以有许多古代建筑都是符合斐波那契数列的。例如,著名的古希腊帕特农神庙,便是依照所谓的“黄金矩形”建立的。
黄金矩形有一个特定的比例。矩形短边与长边的比率等于矩形长边与两条边之和的比率。也就是说,如果我们假设一个黄金矩形宽为A,长为B,那么A与B的比值等于B与(A十B)的比值。
如果我们成对地抽取斐波那契数列中连续的数,它们的比值将会越来越接近黄金比率。比如我们从1, 1, 2, 3, 5, 8,13, 21, 55,89,144, 233中,抽取13/21的比值为0.619047,而当我们抽取144/233时,得到的比值为0.618037。在斐波那契数列中,取越靠后的成对数的比值就越接近理想的黄金比率0.618034。
学者们研究了古代的建筑,发现在许多地方都符合黄金比率(又称为黄金分割率)。它们的矩形长宽比大致等于0.618或者其反面1.618。有时候,这个比率仅仅是近似值,比如3/5(等于0.6)或者5/8(等于0.625),但是这种近似·比率依然能够唤起人类视觉的美好感受。黄金比率也应用于现代建筑之中,比如修建于纽约的联合国大厦。从文艺复兴到19世纪的印象画派以后,黄金分割率都被广泛应用于绘画领域。我们甚至还能够从日常事物中找到黄金·比率的这种悦人特性的应用,比如长宽分别为3,5或5,8英寸的索引卡片。
音阶等级,也与斐波那契数列相关。最常见的是自然音阶,采用八个音(称为八度,用八个音标记)。许多民族音乐则采用五度音阶(用五个音标记),而更复杂的古典音乐和当代音乐则使用了十三度音阶(用十三个音标记)。而5,8,13等数字是斐波那契数列中的一部分。

这是一种内在的和谐吗?
在19世纪后期,一位德国的心理学家古斯塔夫·费希纳(GustavFechner)测量了日常生活中各种符号、标签和其他物品上的矩形,发现其中大多数都近似的符合黄金比率。费希纳还测量了数百人对于符合黄金比率的矩形和随机比例的矩形的反应,发现人们更加喜欢符合黄金分割率的矩形。现代的符号设计者、标签制作者,甚至网页设计者都广泛地运用着黄金比率。
为什么人们更加喜欢黄金比率和符合黄金比率的矩形呢?许多研究者正致力于研究这些问题。或许是因为人们在自然界中更容易看到这样的图形和比率,所以重新看到它们时,感到舒服而自然。或许是我们的神经系统中存在着某种特定结构,使我们对这种比率更加敏感。对于这一切的内在机理尚不清楚。但是,显而易见的是,古代建筑家和中世纪的数学家们(比如来自比萨的莱昂纳多)已经认识到数字的力量以及它们之间的关系,并以此去描述自然,促进艺术和建筑的繁荣。
莱昂纳多的遗产
来自比萨的莱昂纳多,斐波那契数列和黄金比率,共同架起了一座贯通古今的数学桥梁。尽管我们对这位数学先驱的生平细节知之甚少,但他不朽的著作仍在广为流传,并培育了世人对于数学的兴趣,激发了人们观察和探索自然奥秘的热情。这种对于世界本质结构(包括对于人类自身)的好奇心,开启了一个新的时代—文艺复兴。这个时代发端于意大利,大约从14世纪持续到15世纪,席卷并繁荣了整个欧洲。
精妙绝伦的内在结构和探索世界的强大力量,注定了数学在这场崭新的科学革命中必定扮演关键的角色。它深刻地影响着艺术、建筑、工程技术、物理科学和医学等众多领域。莱昂纳多发现的简约模式和黄金比率仅仅是为未来数学领域拉开了一个序幕。
Via:《数学:描绘自然与社会的有力模式》 (美)哈里·亨德森著 王正科 赵华 译
原文有节选
金融工程, 数学算法
